AOC23 - 7 December
Good Morning. I have a confession to make. After day 6, I wanted to reiterate day 5, but first did part 2 of day 2, so ran out of time when I started reimplementing day 5's new algorithm. However I am positive this time that I am on the right track (I just need to figure out now how to navigate between the range gaps mathematically) .
If the trend predictions on Reddit are right, today I am in for a spin again.
After yesterday's walk through the park I anticipate the gates to Mordor today.
For my Sanity let's have a quick peek at my input today:

Letters. First impression: cryptography.
Oh no.
Let's read the text.
Its worse:
Poker.
- We have a list of Hands made of 5 cards
- Each hand has a bid assigned
- We need to sort the hands in order of their rank
- Then multiply each hand's bidding by their rank
- And sum the cards
Also, why are these elves playing games all day at any occasion, and in the most inconvenient circumstances? No wonder everything breaks down. Anyway here is the algorithm:
type alias Hand = (List Char, Int)
solve1 : String -> Int
solve1 str =
parse str |>
List.sortWith compareHands |>
List.indexedMap (\i a -> (i + 1) * Tuple.second a) |>
List.sum
parse : String -> List Hand
compareHands : Hand -> Hand -> Order
We start from the end again, and implement the high level algorithm as I have listed it. I assume that the List Char in the Hand tuple is going to become something a bit more elaborate. But I have learned my lessons about overdesigning my Type system too early in the race. So now we have to figure out how to parse a hand, and then sort it by some ruleset.
Can't read my, can't read my, Poker Hand
What a fun title for a chapter about parsing symbols representing poker hands.
type alias Hand = (List Card, Int)
type Card = A | K | Q | J | Number Int
parse : String -> List Hand
parse str =
let
parseCard char =
case char of
'A' -> Just A
'K' -> Just K
'Q' -> Just Q
'J' -> Just J
'T' -> Just <| Number 10
c ->
String.fromList [c] |>
String.toInt |>
Maybe.andThen
(\a ->
if a > 1 && a < 10 then Just (Number a) else Nothing)
parseHand line =
case (String.split " " line) of
[a] -> (String.toList a |> List.map parseCard |> Maybe.values, 0)
a::b::_ ->
( String.toList a |>
List.map parseCard |>
Maybe.values, String.toInt b |>
Maybe.withDefault 0)
_ -> ([], 0)
This is my parsing function. I am becoming more comfortable with writing the logic of one algorithm in one function definition while keeping clarity. First we define a type card, which can be any of the figures or a number between 2 and 9, or the symbol T which also results in a number: 10. Then I parse each line, splitting it in half on a space and parse the cards and assign them the bid.
This is the output if you are wondering:
From Ace to King, to Peasant
Now we estimate our hand. I think I will fold my List of cards (which sounds quite controversial in a program about poker, but I am referring to the higher-ordered function here). Instead of comparing cards back and forth, I will just look if I find pairs, triplets, full houses or quadruplets.
compareHands : Hand -> Hand -> Order
compareHands hand1 hand2 =
let
valueHand1 = rankHand hand1
valueHand2 = rankHand hand2
(cards1, _) = hand1
(cards2, _) = hand2
in
if valueHand1 == valueHand2
then compare (List.map cardValue cards1) (List.map cardValue cards2)
else compare valueHand1 valueHand2
cardValue : Card -> Int
cardValue card =
case card of
Number n -> n
J -> 11
Q -> 12
K -> 13
A -> 14
rankHand : Hand -> Int
rankHand hand =
let
(cards, _) = hand
frequencies =
List.foldl
(\card matches ->
case (Dict.get card matches) of
Nothing -> Dict.insert card 1 matches
Just n -> Dict.insert card (n + 1) matches
)
(Dict.fromList [])
cards
estimatePlay listOfMatchedCards =
case listOfMatchedCards of
-- 5 of a Kind --
[a] -> let (crd, n) = a in cardValue crd + 500
[(crd1, n1), (crd2, n2)] ->
if n1 > 3
-- 4 of a Kind ---
then cardValue crd1 + 200
-- Full House --
else cardValue crd1 + cardValue crd2 + 90
[(set1, n1), (set2, n2), _] ->
if n1 > n2
-- Three of a Kind --
then cardValue set1 + 60
-- Double Pair --
else cardValue set1 + 20
-- Pair --
(set1, n1)::[_, _, _] ->
cardValue set1
-- None --
_ -> 0
in
Dict.toList frequencies |>
List.sortBy Tuple.second |>
List.reverse |>
estimatePlay
I group the cards by their frequency, then I convert the dictionary back to a list of tuples, so I can pattern match over list, essentially giving me all the cases, with the exception of double pair (2, 2, 1) and triplet (3, 1, 1), aswell as 4 of a kind (4, 1) and full house (3, 2) where I have to branch further.
(In addition I add the value of the card, so that a triple K is > then a triple 9. I found out later, that this is not necessary, first running in a loop for a while.)
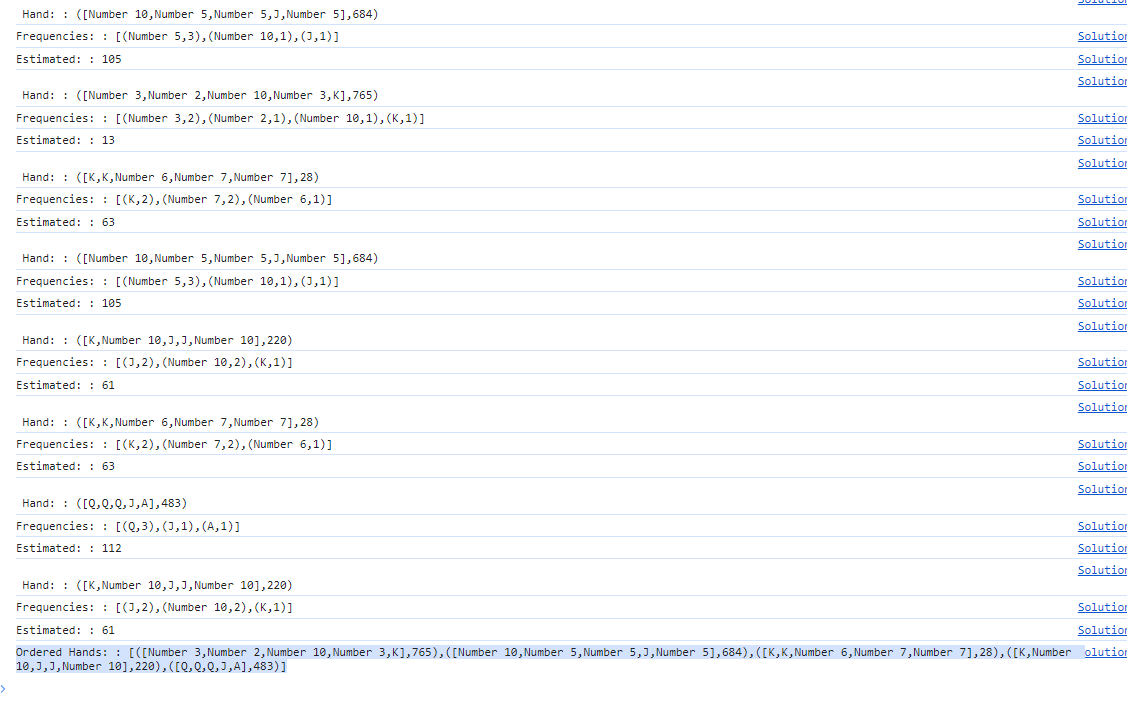
somehow my sorting is messed up, eventhough the rules seem to be correct.
I read the prompt again. On a tie of the same play set the highest card rule is active, so the figure / value of the play set is irrelevant. Nice, 2 hours wasted on bug hunting, which could have been solved by reading more carefully. However after fixing that mistake the output was still invalid.
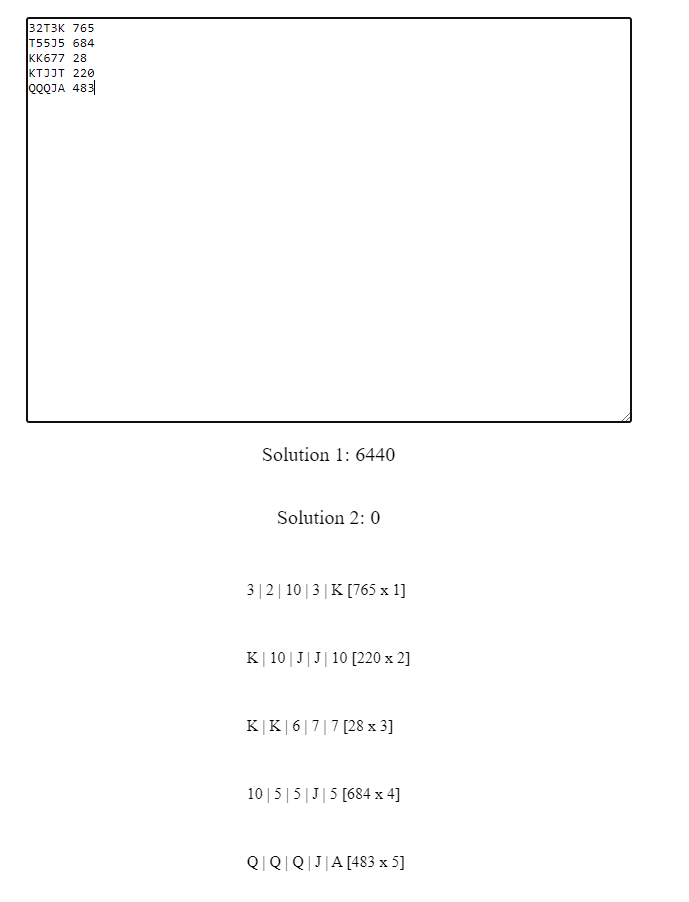
My Sample input works. And I am starting to lose hope. Reading the entire prompt again. Didn't miss anything this time.
Somehow by changing this
...
[(set1, n1), _, _, _] ->
1
-- None --
_ -> 0
It worked

Part Two
Nice curve ball, we have magic Jacks now, that can impersonate any other card. However I don't really care because it is irrelevant which card it impersonates. So it is a matter of checking what the current playset case is, and if jacks are inside of the other groups we then interpolate to the next best result.
cardValue : Card -> Int
cardValue card =
case card of
Number n -> n
J -> 1
Q -> 12
K -> 13
A -> 14
First let's devalue Jacks. And now for what I think is just beautiful.
...
estimatePlay listOfMatchedCards =
case listOfMatchedCards of
-- 5 of a Kind --
[_] -> 10
[(set1, n1), (set2, _)] ->
if n1 > 3
-- 4 of a Kind ---
then 8 + (if jr && (set1 == J || set2 == J) then 2 else 0)
-- Full House --
else 6
+ (if jr && set1 == J then 4 else 0)
+ (if jr && set2 == J then 2 else 0)
[(set1, n1), (set2, n2), (set3, _)] ->
if n1 > n2
-- Three of a Kind --
then 4 + (if jr && set2 == J then 4 else 0)
-- Double Pair --
else 2
+ (if jr && (set2 == J || set1 == J) then 8 else 0)
+ (if jr && set3 == J then 4 else 0)
-- Pair --
[(set1, _), (set2, _), (set3, _), (set4, _)] ->
1
+ (if jr && ( set2 == J || set3 == J || set4 == J) then 1 else 0)
+ (if jr && set1 == J then 3 else 0)
-- None --
_ -> 0
I can just add an optional jack rule which based on its occurrence in my existing patterns modifies the points and therefor promotes my hands.

There seem to be some more hiccups now (being able to search for J on a nicely spaced website helped greatly this time), which only show in the "real" input.
After some head scratching and multiple failed sanity checks, I found the "equation" to happiness:
...
-- 5 of a Kind --
[_] -> 10
[(set1, n1), (set2, _)] ->
if jr && (set1 == J || set2 == J)
then 10
else
if n1 > 3
-- 4 of a Kind ---
then 8
-- Full House --
else 6
[(set1, n1), (set2, n2), (set3, _)] ->
if n1 > n2
-- Three of a Kind --
then 3
+ (if jr && (set1 == J || set2 == J || set3 == J) then 5 else 0)
-- Double Pair --
else 2
+ (if jr && (set2 == J || set1 == J) then 6 else 0)
+ (if jr && set3 == J then 4 else 0)
-- Pair --
[(set1, _), (set2, _), (set3, _), (set4, _)] ->
1
+ (if jr && (set1 == J || set2 == J || set3 == J || set4 == J)
then 2 else 0)
-- None --
list ->
if jr
&& (List.filter (\a -> Tuple.first a == J) list |> List.length) > 0
then 1
else 0
...
Takeaway
Honestly, I think I did well today but then tripped up on small details (in part due to overlooking some details in the prompt which I misinterpreted) which were hard to identify in the log. Similar to day 3, finding the right output format to analyze the patterns was essential today. I am glad that I did. Also I think that in today's solution, pattern matching was shining. I think the frequency grouping with the pattern matching was pretty smart, which enabled me to implement the Joker rule quickly. Now I have to adapt my future elm framework so that I can switch between part 1 and 2 and this is also reflected in my view. Because today I only could display one of the outcomes simultaneously, and I think it adds some nice interactivity.
See you on the next challenge!