AOC23 - 6 December
Yesterday's challenge and resulting session taught me a valuable lesson. Efficiency.
Write less. Code less. Be happier.
What broke my neck yesterday was my bottom up approach, starting to model every single component as its own idiomatic data concept. Also, while it helps with the reasoning, translating the entire puzzle input to a more readable data structure and keeping it in memory at once, was also not such a good idea. So today :
- I am not using data structure to store the entire input, instead use the power of functional programming, mainly referential transparency and the power of composition to create my abstraction while also implementing the algorithm
- I will start at the end and work my way from the end to the bottom components
- I will be as concise as possible. This also includes my write ups
The Puzzle
Determine the number of ways you could beat the record in each race. What do you get if you multiply these numbers together?
This is the goal.
So micro-boat races. Sounds fun. And no numbers, that by themselves cause a stack overflow, or break my sanity for that matter. At least as far as I can tell. Let's not jinx it.
Let's break it down shall we?
- We have a list of records showing the amount of time allowed for the race (including time to charge up the boat, like a wind-up toy) and the related best distance.
- As I said, in the allowed time you need to charge up the boat and on release the boat goes as far as it can with that charge
- Charging can only happen before the start of the race
- The boat has a starting speed of 0 mm/ms and for each ms we press we can add 1mm/ms
- I have to determine all possible combinations of times per race to beat the record giving me a range of min time to max time, resulting in the number of ways (discrete 1 ms steps)
- Then multiply all the counts together for the final result.
The input is incredibly sobering today, as compared to the monster I got yesterday
Time: 54 70 82 75
Distance: 239 1142 1295 1253
But I guess looks can be deceiving.
The Algorithm
solve1 : String -> Int
solve1 str =
parse str |>
List.map countOptions |>
List.product
type alias Race = (Int, Int)
parse : String -> List Race
parse str = []
countOptions : Race -> Int
countOptions r = 0
Star of the show this time is our countOptions algorithm. I will do pincer maneuver, start from 0 and the max time and move stepwise up and down. As soon as it hits the record it will stop.
countOptions : Race -> Int
countOptions r =
let
(time, dist) = r
moveRange range =
let
(min, max) = range
newmin = min + 1
newmax = max - 1
newRange =
( if newmin > 0 && distance time newmin <= dist then newmin else min
, if distance time newmax > dist then newmax else max)
in
if newRange == range then range else moveRange newRange
(minWin, maxWin) = moveRange (0, time)
in maxWin - minWin
I've decided to do a negative check to reach the boundaries from the outside, as soon as my min or max beat the distance I jump out of the loop get the difference and that's the amount of options in-between that win. At least that's what I hope.
distance : Int -> Int -> Int
distance totalTime chargeTime = (totalTime - chargeTime) * chargeTime
This is the distance function. Which is pretty self-explanatory.
Now let's parse the input!
Parsing
We only need the number series on row 2 and 3 and zip them to tuples. Easiest parse in my life.
parse : String -> List Race
parse str =
let
lines = String.lines str
in
case lines of
[first, second, third] -> List.zip (parseNums second) (parseNums third)
_ -> []
The only hiccup I encountered here was that, I first tried to
List.map parseNum [second, third] |> List.zip
But List.zip expects them to be two separate arguments. In Lisp like language in such a case I could just use the spread (unquote splicing '~@') operator to disassemble a list of arguments and apply them, or I could use meta-function such as 'apply' to apply a list of values to a function. This is missing in this current flavor of functional programming.
That's all, lets test and debug
Test and Debug
Putting in the sample data I got: 1. Uuuuu, something is not right.
Nevermind, that was a parsing mistake. The input only has two rows, so I triggered my edge case and returned an empty list.
Ok still not a match
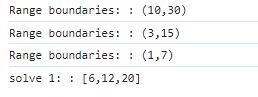
I am off by a big margin. Let's investigate
...
newRange =
( if distance time newmin <= dist then newmin else min
, if distance time newmax <= dist then newmax else max)
in
if newRange == range then range else moveRange newRange
(minWin, maxWin) = moveRange (0, time)
in maxWin - minWin - 1
I think I had my logic the other way around. I was under the assumption that the maxTime wins by default, but that value refers to how long I press the button, so I had a false negative. Instead I switched it and also fixed the counting aspect substracting one.

There you go!
Ok, let's try the real input.

Yay, first try! (On the real data).
Part two
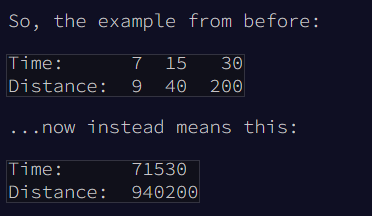
Hehe, I have an idea.
replace : String -> String -> String -> String
😁
solve2 : String -> Int
solve2 str = solve1 <|
Regex.replace
(Maybe.withDefault Regex.never <| Regex.fromString "[^\\S\\r\\n]")
(\_ -> "") str
That should do it.
Wait...
Will this kill my processor / memory again? Oh no! -> 239114212951253 / 54708275
Like stealing an ice cream from a baby. (Be adviced. I do not condone this sort of behavior)
Takeaway
I think I started thinking more in terms of the problems requirement to find the ideal middle ground between readability, clarity and efficiency this time and ended up with a relatively concise and elegant algorithm. It was so well setup, that just changing the input data still made it work, and that relatively quickly. In parts this is also due to the amazing pipeline like paradigm you work with in these kind of languages. I love this more and more. This even motivates me enough to try and apply this mentality to yesterday's failed challenge again and see if there is a way to avoid having to store all of those gigantamax ranges and avoid having to enumerate them.
See you on the next challenge!